✅ 🇬🇧 Logical Data Model (LDM)
| Catégorie | Cours |
|---|---|
| Ordre d'apprentissage | 14 |
| Statut | préparé |
Cours de Julie Chaumard
LDM
Introduction to the Logical Data Model (LDM)
The previous chapter established the Conceptual Data Model (CDM) of the Marathon database.
This chapter explains the next step: the development of the Logical Data Model (LDM).
As with the vast majority of databases, the Relational Model is chosen as the Logical Data Model.
Principles of the relational model
The principles of the relational model were defined by the Englishman Edgar Frank Codd,
a researcher at IBM®, in the 1970s.
These principles consist of formalizing:
📌 The data storage structure
This organization is based on the use of two-dimensional tables.
Its advantage is to ensure consistency and absence of redundancy of values.
A database table is organized in rows and columns,
which creates a two-dimensional structure:
- Columns (or attributes) represent the characteristics of the data (e.g.: ID, Name, Age, City).
- Rows (or records) contain the values associated with each element.
📌 Data manipulation
The querying of relational databases is based on the theory of relational calculus
and relational algebra.
"Edgar Frank Ted Codd (1923-2003) was a British computer scientist considered the inventor of the relational model for RDBMS."
Theory of relational calculus and algebra
Functional dependencies
Functional Dependencies (FD) in the Relational Model
The objective is to define links between metadata in the dictionary seen in the previous chapter.
For this purpose, the mathematical notion of functional dependency is used.
In the context of the relational model, a metadata corresponds to an attribute.
📌 Definition of Functional Dependency (FD)
There is a functional dependency between two attributes Aᵢ and Aⱼ,
if for a known value of Aᵢ, the corresponding value of Aⱼ is determined.
We note:
Aᵢ → Aⱼ
Similarly, there is a functional dependency between a list of attributes
(Aᵢ, … Aₙ) and an attribute Aⱼ,
if for a combination of values of (Aᵢ, … Aₙ), the value of Aⱼ is determined.
We note:
(Aᵢ, … Aₙ) → Aⱼ
📌 Notation and Role of Attributes in an FD
In an FD (Functional Dependency) noted Aᵢ → Aⱼ:
- Aᵢ is considered as the source (determinant).
- Aⱼ is considered as the target (dependent).
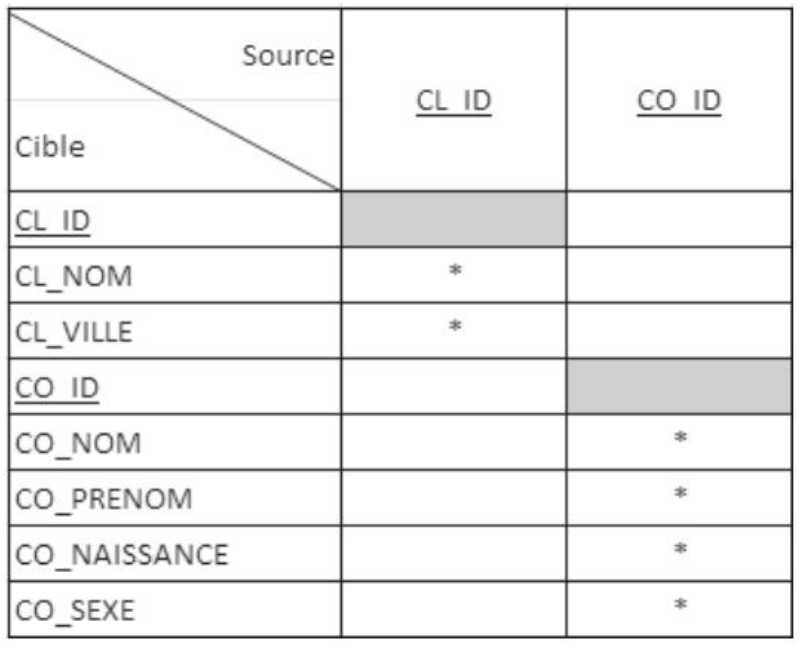
📌 Examples of Existing Functional Dependencies
The following FDs are valid:
- CO_ID → CO_NOM
- CO_ID → CO_PRENOM
- CO_ID → CO_NAISSANCE
- CL_ID → CL_NOM
📌 Examples of Non-existent Functional Dependencies
Knowledge of the subject allows us to understand that certain FDs do not exist,
such as the one between CO_ID and AD_LICENCE.
📌 Explanation:
A runner can have multiple license numbers during their career.
Therefore, there is no univocal relationship between CO_ID and AD_LICENCE.
Identifier
Definition of the Identifier in the Relational Model
This notion, very intuitive, must be defined using Functional Dependencies (FD).
📌 Mathematical Definition
Let E be a set of attributes {A₁, A₂, ..., Aₙ} and I a subset of E.
I is an identifier if, for any attribute A belonging to E, the following relation is verified:
I → A
In the context of the relational model, the identifier is called the primary key.
A primary key can be composed of multiple attributes.
📌 Notation:
The formalism requires underlining the attributes that make up the primary key.
📌 Example of Primary Key
Consider the set of attributes:
{CO_ID, CO_NOM, CO_PRENOM, CO_NAISSANCE, CO_SEXE}
The attribute CO_ID is considered a primary key because it dominates the others.
The associated functional dependencies are:
- CO_ID → CO_NOM
- CO_ID → CO_PRENOM
- CO_ID → CO_NAISSANCE
- CO_ID → CO_SEXE
Matrix of functional dependencies
Relation
The Relation in the Relational Model
The relation is the basic concept of the relational model.
To define it, the notions of domain and Cartesian product are necessary.
📌 Definition of Domain
A domain can be applied to a column of a table.
In other words, a domain corresponds to the set of possible values
that a column of a table can contain.
📌 The Cartesian Product
The Cartesian product of two domains D₁ and D₂ is the set of all possible pairs
(V₁, V₂) where:
- V₁ ∈ D₁
- V₂ ∈ D₂
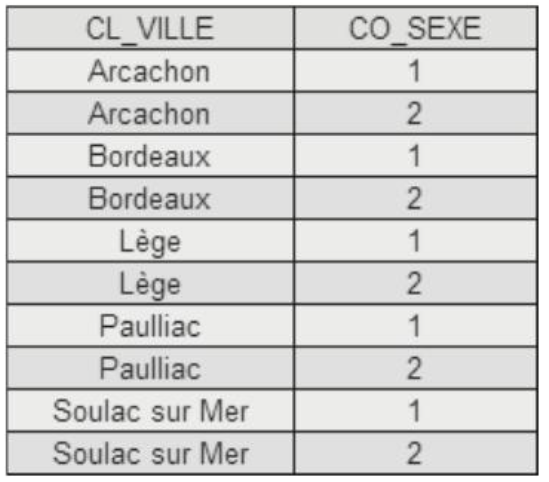
Example:
The Cartesian product of the domains of attributes CL_VILLE and CO_SEXE
associates to each city value all gender values.
📌 Definition of a Relation
A relation is a subset of the Cartesian product of a list of domains.
In other words, a relation is a two-dimensional table.
In the context of a relation:
- A column of the table is called an attribute.
📌 Formalism for presenting a relation:
<Relation name> (<Attribute name 1>, <Attribute name 2>, …)
First normal form
First normal form (1NF)
A relation is in first normal form if:
- It has a primary key that dominates all fields that compose it.
- Every attribute it contains is non-decomposable.
Using the FD matrix allows defining relations in first normal form.
Example
Counter-example of the first normal form
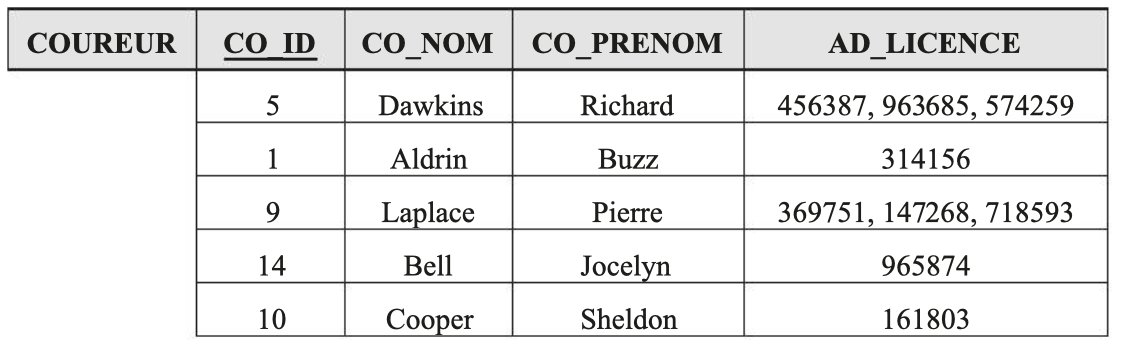
Consider the relation RUNNER (CO_ID, CO_NOM, CO_PRENOM, AD_LICENCE) representing information about a runner and their club membership licenses.
Representation of the relation with occurrences:
In this example, the attribute AD_LICENCE represents a set of license numbers of a runner.
These values are therefore decomposable into multiple numbers and there is no uniqueness of information.
This relation does have a primary key, but there is no functional dependency (FD) with the attribute AD_LICENCE.
This relation is therefore not in first normal form.
For this relation to be in first normal form, it must be in the following form:
RUNNER (CO_ID, CO_NOM, CO_PRENOM)
Second normal form
Second normal form (2NF)
The second normal form is defined from the first.
A relation is in second normal form if, and only if:
- It is in first normal form.
- Every attribute not belonging to the primary key does not depend on a part of the key.
By its definition, the second normal form applies only to relations
whose primary key is composed of multiple attributes.
Example
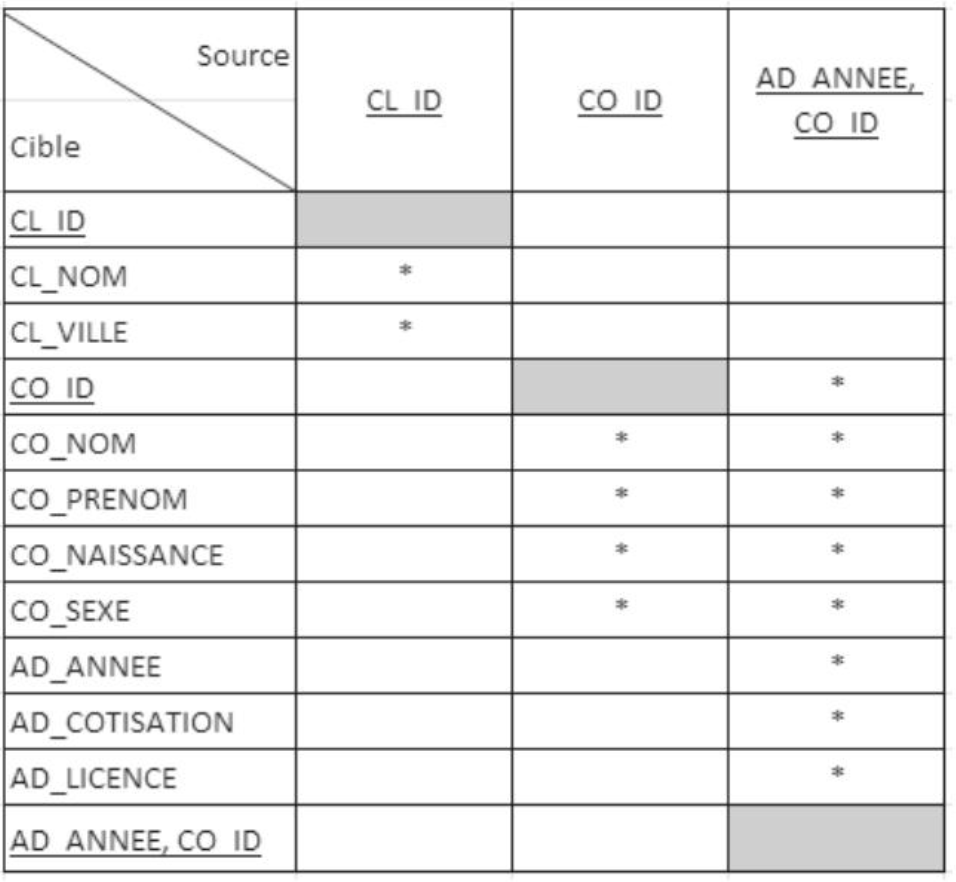
In order to define FDs whose target is AD_COTISATION and AD_LICENCE,
it is necessary to concatenate the attributes CO_ID and AD_ANNEE.
Consider the relation
RUNNER (CO_ID, AD_ANNEE, CO_NOM, CO_PRENOM, CO_NAISSANCE, CO_SEXE, AD_COTISATION, AD_LICENCE)
The primary key of this relation is composed of the attributes CO_ID and AD_ANNEE
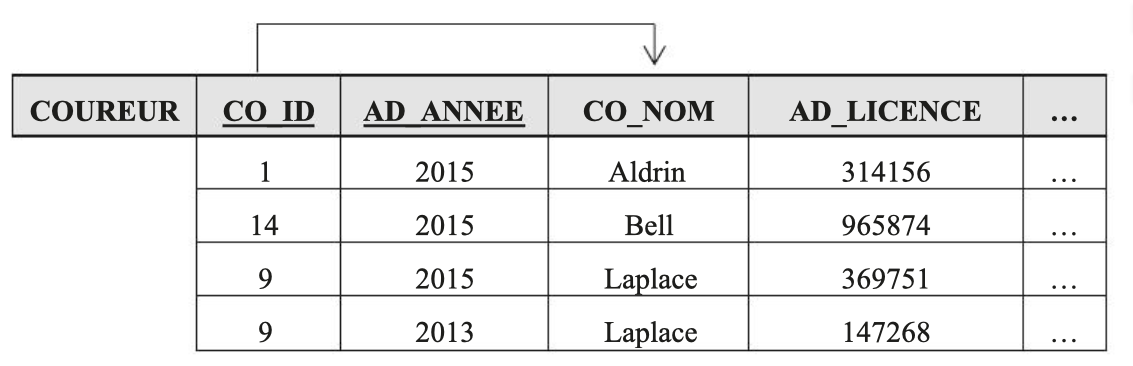
In this example, the attribute CO_ID is part of the primary key and its values determine the values of the attribute CO_NOM, unlike AD_LICENCE which is determined from the attributes CO_ID and AD_ANNEE. The relation is therefore not in second normal form. The solution consists of decomposing the RUNNER relation into two relations: RUNNER and MEMBERSHIP. The latter recording information for a given year:
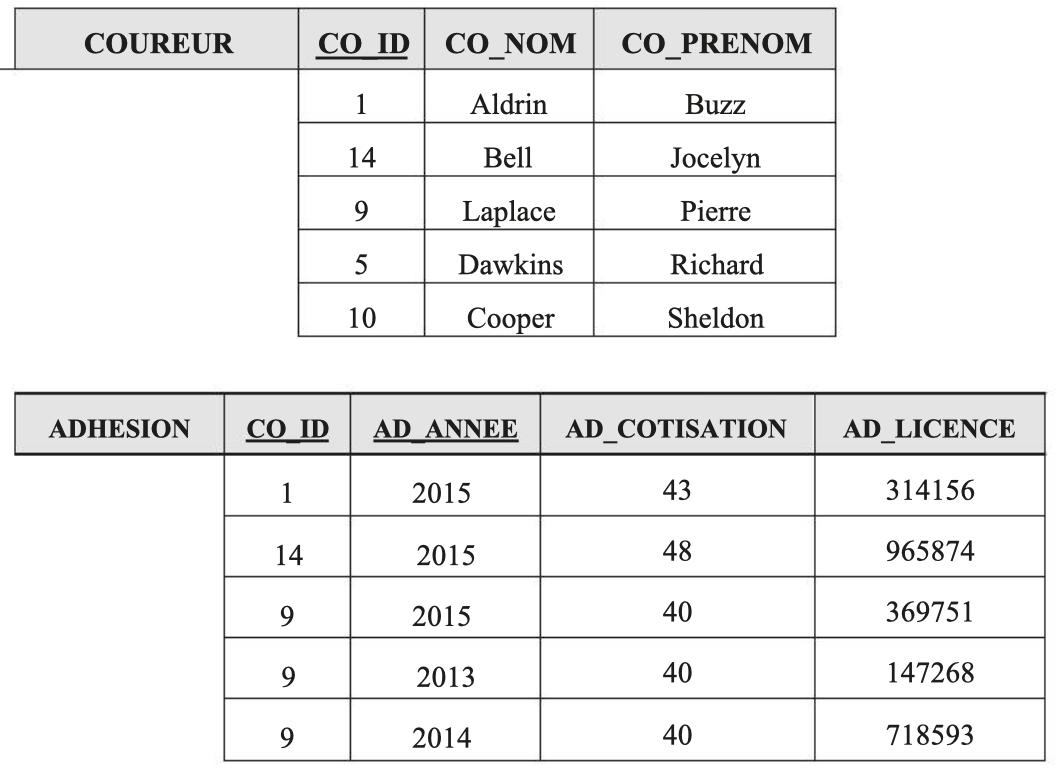
RUNNER (CO_ID, CO_NOM, CO_PRENOM, CO_NAISSANCE, CO_SEXE)
MEMBERSHIP (CO_ID, AD_ANNEE, AD_COTISATION, AD_LICENCE…)
Indeed, for the identifier of the RUNNER relation to be minimal, information relating to a year must be removed. The relations in second normal form are then:
Decomposition respecting the second normal form:
Third normal form
Transitivity: if A → B and B → C then A → C
The third normal form is defined from the second. A relation is in third normal form if, and only if:
- It is in second normal form.
- Any attribute not belonging to the primary key does not depend on another non-key attribute.
The third normal form eliminates transitive FDs in a relation.
Counter-example of the third normal form
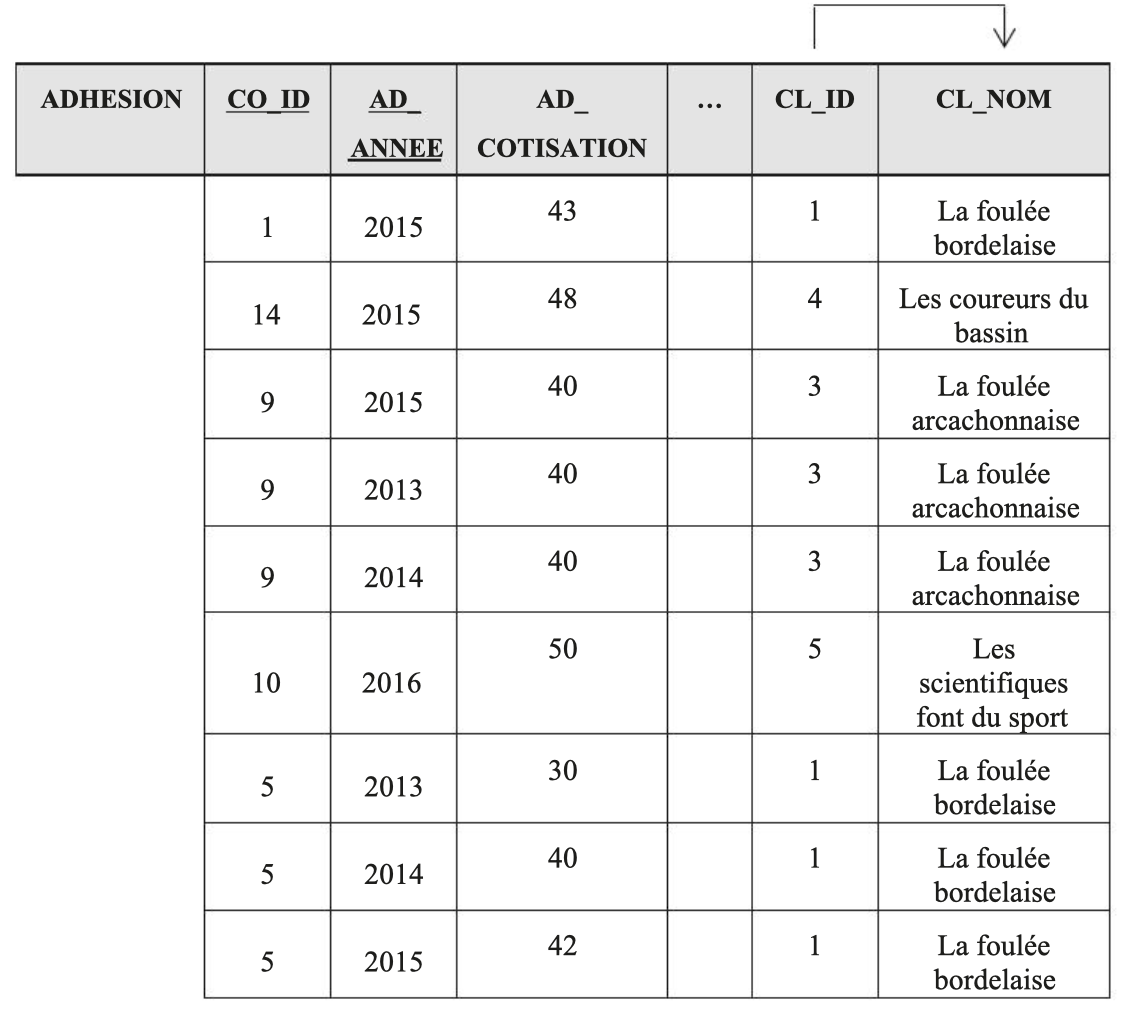
Consider the relation MEMBERSHIP (CO_ID, AD_ANNEE, AD_COTISATION, …, CL_ID, CL_NOM). Representation of the relation with occurrences:
In this relation, there is an FD having as source the attribute CL_ID and as target the attribute CL_NOM. Since these attributes are not part of the primary key, this relation is not in third normal form.
The solution consists of decomposing the MEMBERSHIP relation into two relations: MEMBERSHIP and CLUB. The final modeling of the CLUB, RUNNER, MEMBERSHIP relations is as follows.
Decomposition respecting the third normal form
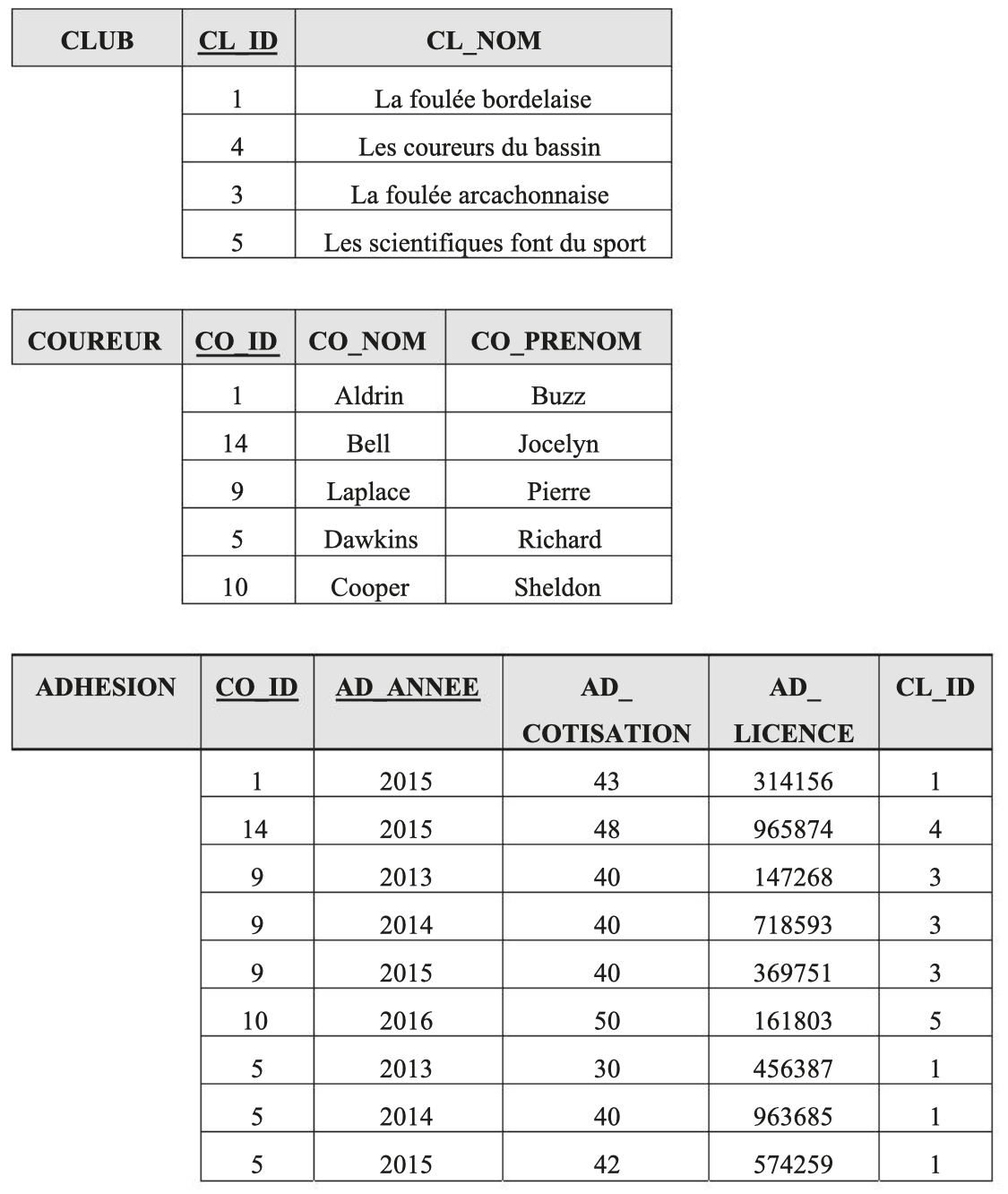
Transition from CDM to Relational Model
This paragraph presents how to move from the Conceptual Data Model to the Relational Model
The logical model consists of transforming the CDM, which is independent of technical implementation, into a model that will be implemented in a computer tool. Each entity becomes a relation.
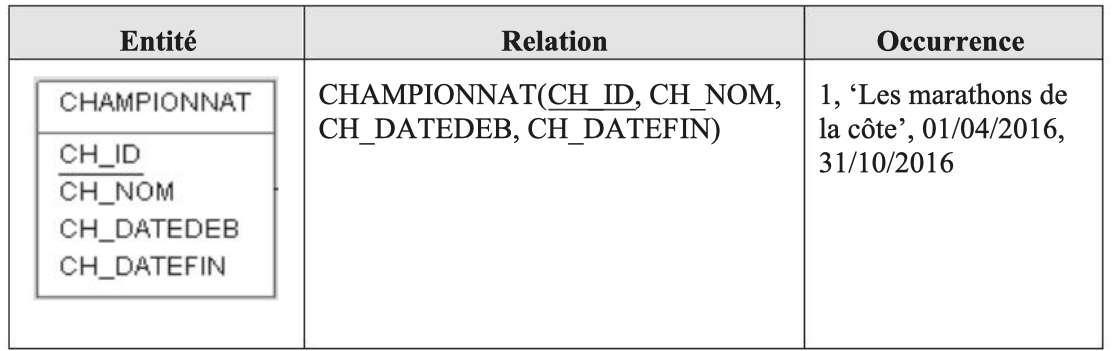
Similarly, we define the EVENT relation from the corresponding entity. This gives:
- EVENT (MA_ID, MA_NOM)
- CHAMPIONSHIP (CH_ID, CH_NOM, CH_DATEDEB, CH_DATEFIN)
Thus, relations are established from entities. Now we need to "translate" the associations according to the cardinalities used. Two cases are distinguished according to the maximum value of the cardinality.
A cardinality with a maximum equal to 1
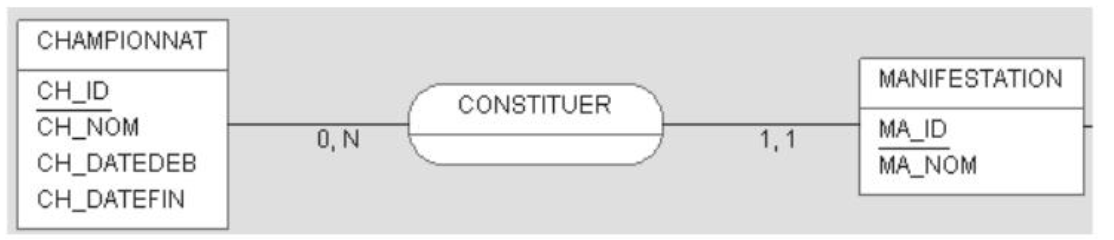
In this case, an attribute is added to the entity/relation with this cardinality. This new attribute references the identifier of the opposite entity/relation. This is a foreign key, i.e., a reference to a primary key. The convention prefixes the attribute with the symbol #.
For this association, the field MA_CHAMP_FK is added to the relation
EVENT (MA_ID, MA_NOM, #MA_CHAMP_FK)
A cardinality with a maximum equal to N
In this case, a new relation is created with the name of the association. As was done in the previous case, foreign keys are created from all primary keys of the linked relations. The primary key of this new relation is composed of all newly added foreign keys. As a result, the added attributes are both foreign keys and parts of the primary key.
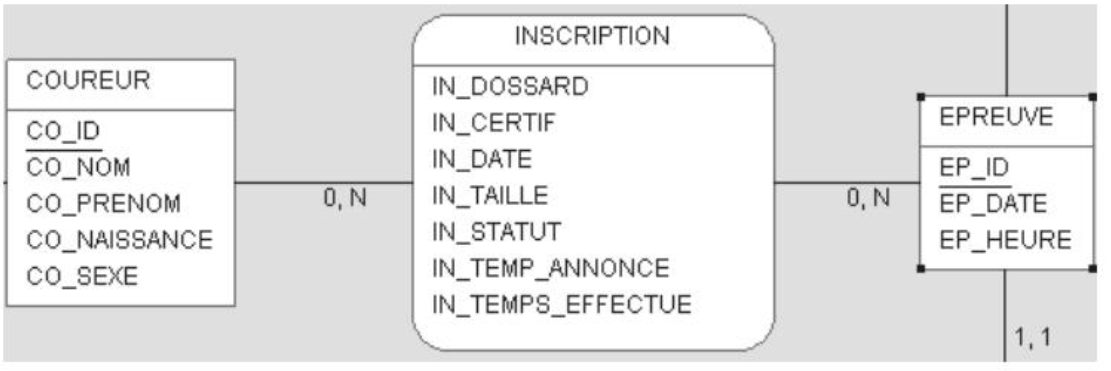
The REGISTRATION relation is added to existing ones:
- REGISTRATION (#IN_COUREUR_FK, #IN_EPREUVE_FK, IN_DOSSARD, IN_DATE, IN_CERTIF, IN_TAILLE, IN_STATUT, IN_TEMP_ANNONCE, IN_TEMP_EFFECTUE)
- EVENT (MA_ID, MA_NOM)
- CHAMPIONSHIP (CH_ID, CH_NOM, CH_DATEDEB, CH_DATEFIN)
Case 0,N or 1,N
What would be the ID of the REGISTRATION table in the case of (0,N)?
In the case where the relationship between RUNNER and REGISTRATION as well as RACE and REGISTRATIONis (0,N), this means that a registration can exist without being mandatory for a runner or a race.
📌 1️⃣ Choice of ID for the REGISTRATION table
The identifier (primary key) of REGISTRATION must guarantee the uniqueness of records. Several solutions are possible:
🔹 Option 1: Use an auto-incremented ID (recommended)
The most common way is to assign an auto-incremented primary key, independent of foreign keys. This allows having a unique ID for each registration, even if CO_ID or EP_ID are NULL.
CREATE TABLE REGISTRATION (
IN_ID INT PRIMARY KEY AUTO_INCREMENT, -- Unique auto-incremented ID
IN_DOSSARD INT,
IN_CERTIF BOOLEAN,
IN_DATE DATE,
IN_TAILLE VARCHAR(10),
IN_STATUT VARCHAR(20),
IN_TEMP_ANNONCE TIME,
IN_TEMPS_EFFECTUE TIME,
CO_ID INT NULL, -- Optional (0,N)
EP_ID INT NULL, -- Optional (0,N)
FOREIGN KEY (CO_ID) REFERENCES RUNNER(CO_ID),
FOREIGN KEY (EP_ID) REFERENCES RACE(EP_ID)
);
✔ Advantages:
- Independence from foreign keys.
- Allows adding registrations without runner or race (in case they are registered later).
- Simpler SQL queries (e.g.: SELECT * FROM REGISTRATION WHERE IN_ID = 1).
🔹 Option 2: Composite primary key (less flexible)
Another possibility would be to use a composite primary key based on CO_ID and EP_ID. But since the relationship is (0,N), these values can be NULL, which poses a problem because a primary key cannot contain NULL.
❌ This solution is impossible with a (0,N) relationship because CO_ID or EP_ID can be NULL.
If the relationship was (1,N), we could have had a composite primary key like this:
CREATE TABLE REGISTRATION (
CO_ID INT,
EP_ID INT,
IN_DOSSARD INT,
IN_CERTIF BOOLEAN,
IN_DATE DATE,
PRIMARY KEY (CO_ID, EP_ID), -- Impossible in (0,N) because NULL forbidden
FOREIGN KEY (CO_ID) REFERENCES RUNNER(CO_ID),
FOREIGN KEY (EP_ID) REFERENCES RACE(EP_ID)
);
🚨 Why doesn't it work in (0,N)? ➡ A primary key cannot contain NULL values. ➡ In (0,N), CO_ID or EP_ID can be NULL, so they cannot be put in a primary key.
📌 2️⃣ Which solution to choose?
✅ Recommended solution → Option 1: Auto-incremented ID
💡 This allows more flexibility, especially if registrations are created before being associated with a runner or a race.
Conclusion
- In (0,N), we cannot use a composite primary key on CO_ID and EP_ID.
- The best solution is to use an auto-incremented ID (IN_ID) as the primary key.
- The foreign keys CO_ID and EP_ID must be NULLABLE (NULL allowed).
💡 👉 In an LDM, this translates to:
REGISTRATION (IN_ID, IN_DOSSARD, IN_DATE, CO_ID (0,N), EP_ID (0,N))
🎯 So, for a good transition from CDM → LDM, we use a unique ID (IN_ID) in the REGISTRATION table to guarantee the uniqueness of records.
The Marathon database: the LDM
By applying the transformation rules to the conceptual data model of the Marathon database, the following relations are obtained:
- RUNNER (CO_ID, CO_NOM, CO_PRENOM, CO_NAISSANCE, CO_SEXE)
- CLUB (CL_ID, CL_NOM, CL_VILLE)
- RACE (EP_ID, EP_DATE, EP_HEURE, #TY_ID, #MA_ID)
- RACE_TYPE (TY_ID, TY_LIBELLE, TY_DISTANCE)
- REGISTRATION (#CO_ID, #EP_ID, IN_DOSSARD, IN_DATE, IN_CERTIF, IN_TAILLE, IN_STATUT, IN_TEMP_ANNONCE, IN_TEMP_EFFECTUE)
- EVENT (MA_ID, MA_NOM, #CH_ID)
- CHAMPIONSHIP (CH_ID, CH_NOM, CH_DATEDEB, CH_DATEFIN)
- AGE_CATEGORY (CA_ID, CA_LIBELLE, CA_AGEDEB, CA_AGEFIN)
- MEMBERSHIP (#CO_ID, AD_ANNEE, AD_COTISATION, AD_LICENCE, #CL_ID)
Vocabulary
The first part of the chapter details the relational model and helps to better understand the design generally applied intuitively. The second part of the chapter explains how to move from the Conceptual Data Model to the Relational Model. The models have many of their concepts in common but the vocabulary differs. The table below compares the denominations by model.
| CDM | Relation | DBMS |
|---|---|---|
| Entity | Relation | Table |
| Association | Relation | Table |
| Identifier | Primary key | Primary key |
| Foreign key | Foreign key | |
| Attribute, property | Attribute | Column, field |
| Occurrence, instance | Occurrence | Occurrence, record |
Optimization
The previous chapters present the method and the different steps to design a relational database model that conforms to theory and requirements. Before putting this database into production, it is often necessary to go through a phase of complementary analysis to optimize the planned structure in order to adapt it to the real operating constraints. This is what we call design optimization or database structure optimization.
This optimization focuses on two essential points:
- Optimization of the table structure.
- Optimization of field typing.
The previous chapters presented the rules and standards (normal forms) used to design a database adapted to an expressed need and respecting "best practices".
In practice, when implementing a relational database model, it may be necessary to deviate from some of these rules in order to improve the execution speed of queries.
Redundancies
The most common case consists of setting up voluntary redundancies, that is, adding fields containing information that can be deduced from an operation or found in another table in the database.
A very illustrative example of the interest of this kind of practice: the calculation of the bank balance.
There are two methods to calculate the bank balance of an account on the current date:
- Take all debit and credit movements since the account was opened until today and calculate the difference.
| Advantage | Disadvantage |
|---|---|
| The returned value is necessarily correct. | The number of records is constantly increasing. |
- Make an intermediate calculation every month, store it in the database, and start from this point to calculate the balance of the day.
| Advantage | Disadvantage |
|---|---|
| The number of records handled is limited and fairly constant, and thus the execution time of this process varies little. | The previously calculated balance may be incorrect in case of recording movements with an effective date prior to the date of the balance calculation. This can be mitigated by establishing a management rule requiring, for example, a recalculation whenever a movement prior to the balance is added, modified, or deleted. |
After a few years, one can easily imagine which solution is the most efficient. This second method is also used for stock calculations in commercial management applications. For these two examples, the choice of redundancy is also explained by fiscal obligations imposing a "statement" of values at a given date, balance sheet, or tax declaration.
Example
For the Marathon project, in the RUNNER, REGISTRATION, and RACE tables, the age of a runner at the time of a race allows determining their category and, later, their ranking. It can be calculated with the date of birth and the date of the race.
But it is more efficient to calculate the age at the time of registration, thus only once. Therefore, a new field is added to the REGISTRATION table for future uses, particularly to be able to calculate the ranking by category. With the same objective, adding a link with the AGE_CATEGORY table allows
Primary Keys
It was previously explained how to construct tables according to the expressed needs, and how primary and secondary keys are deduced from the links established between these tables. During this analysis, composite keys appeared, that is, keys composed of several fields from the same table.
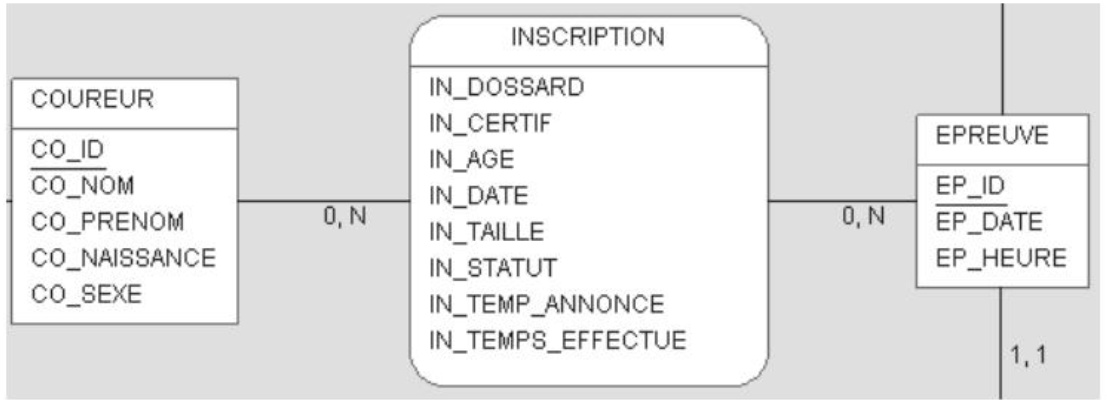
In this excerpt, we can see that the registration is identified by the concatenation of the identifiers of the runner and the race. This solution is the most natural and readable for understanding the table. Depending on the situations and on a case-by-case basis, it may be interesting to replace this composite key with a unique key, called technical, that is, an "ID" field, auto-incremental, and having no logical correspondence with existing fields. This modification can be relevant for the following reasons:
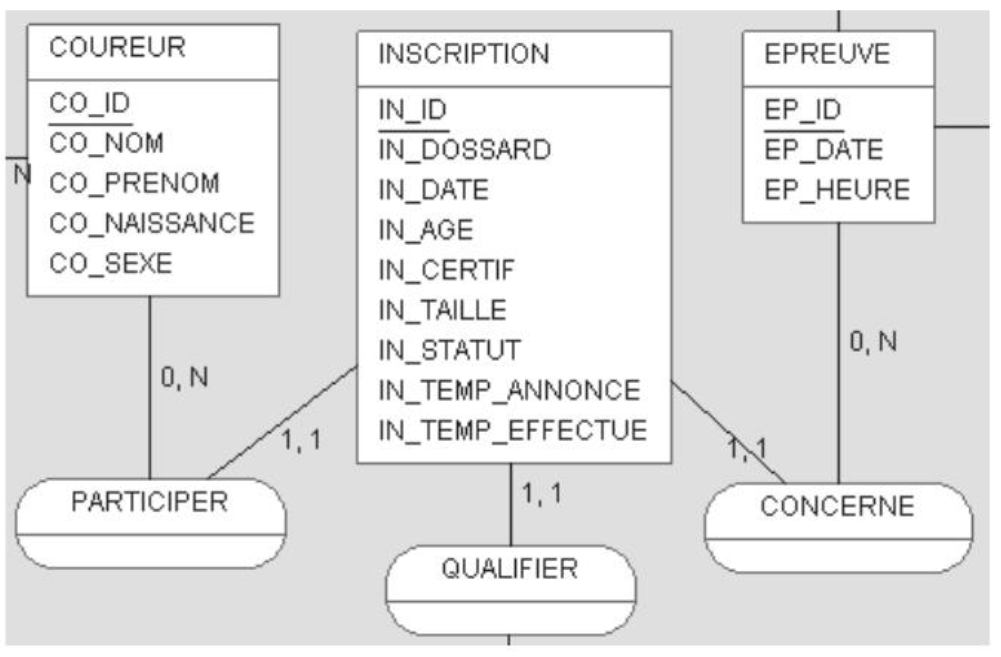
- Simplify the design and reading of queries. In joins or in the WHERE clause, a multiple condition to identify a record is replaced by a single element.
- Speed up processing. The primary key being an index used by the database engine, the search is faster on a unique index than on a multi-field index, especially during searches involving only one part of the key: for example, the number of registrants for a given race.
Based on these principles, the modeling presented previously becomes:
Optimization of Field Types
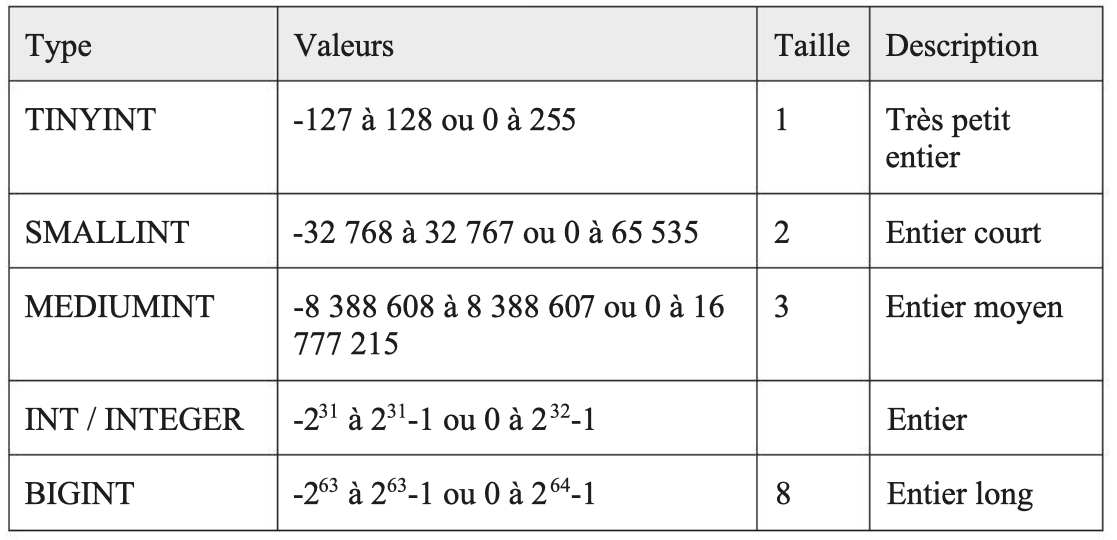
For the same data stored in a field, depending on the chosen type, the space occupied in the database, and therefore the processing time, can vary greatly. It is therefore necessary to pay special attention to the values expected in each field and adapt the data type accordingly.
Here are some simple rules to follow to optimize a database from the design stage.
- For text fields, prefer the VARCHAR type to CHAR because CHAR has a fixed size regardless of the number of characters subsequently recorded.
- VARCHAR(n) stores only the actual length of the string, plus 1 or 2 additional bytes to store the size. • No padding with spaces. • Saves storage space when strings have variable lengths.
- Similarly, for integer type fields, use, if possible, a TINYINT instead of a BIGINT whose storage space is larger.
Final CDM/LDM
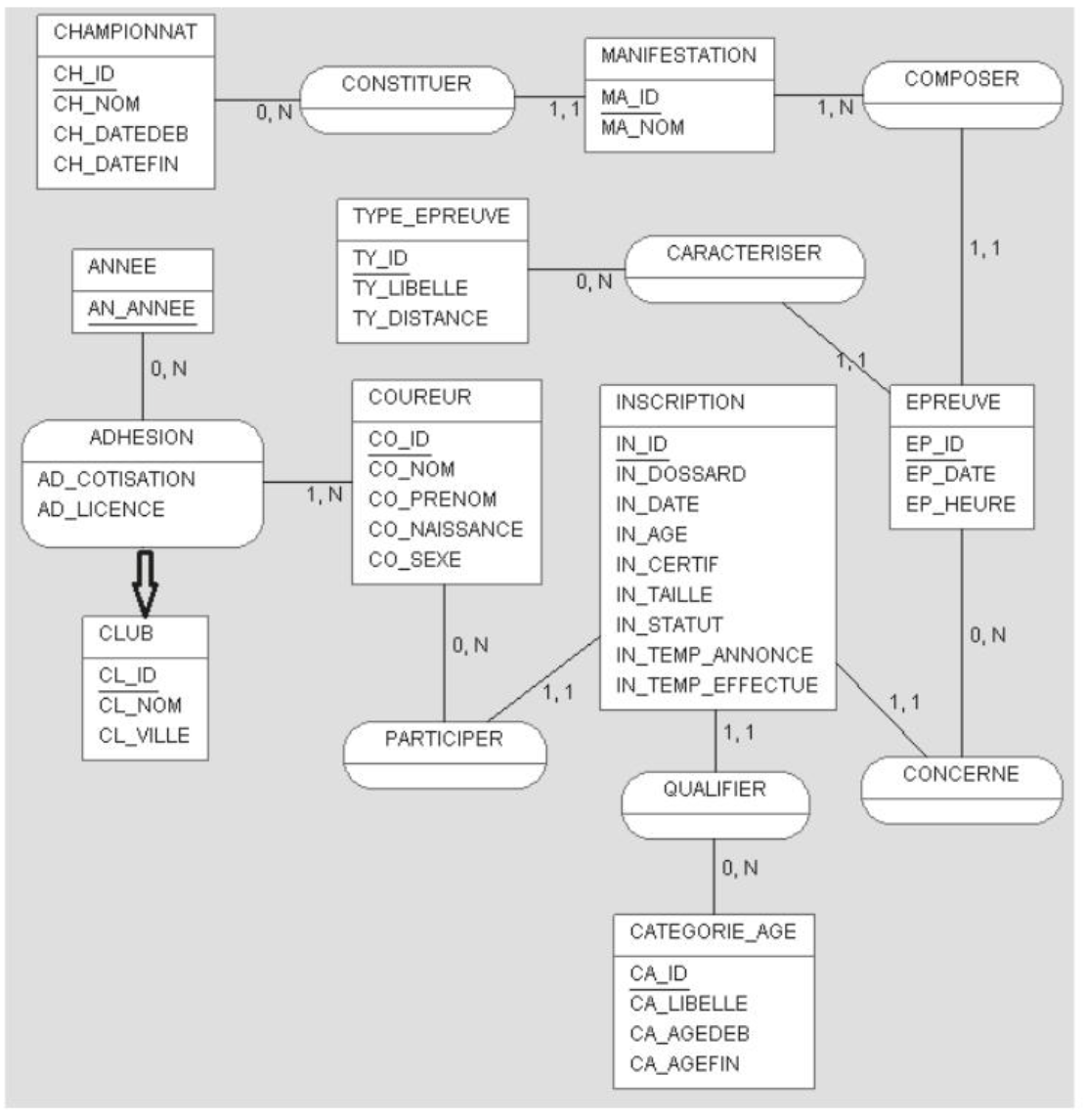
- RUNNER (CO_ID, CO_NOM, CO_PRENOM, CO_NAISSANCE, CO_SEXE)
- CLUB (CL_ID, CL_NOM, CL_VILLE)
- RACE (EP_ID, EP_DATE, EP_HEURE, #TY_ID, #MA_ID)
- RACE_TYPE (TY_ID, TY_LIBELLE, TY_DISTANCE)
- REGISTRATION (IN_ID, #CO_ID, #EP_ID, IN_DOSSARD, IN_DATE, IN_AGE, #CA_ID, IN_CERTIF, IN_TAILLE, IN_STATUT, IN_TEMP_ANNONCE, IN_TEMP_EFFECTUE)
- EVENT (MA_ID, MA_NOM, #CH_ID)
- CHAMPIONSHIP (CH_ID, CH_NOM, CH_DATEDEB, CH_DATEFIN)
- AGE_CATEGORY (CA_ID, CA_LIBELLE, CA_AGEDEB, CA_AGEFIN)
- MEMBERSHIP (#CO_ID, AD_ANNEE, AD_COTISATION, AD_LICENCE, #CL_ID)
Agence digitale Parisweb.art
Tout savoir sur Julie, notre directrice de projets digitaux :
https://www.linkedin.com/in/juliechaumard/